机器学习报告——数据分类的实现

1 数据集 1
2 logistic 回归与神经网络 1
2.1 背景知识 1
2.1.1 线性及 sigmoid 函数 1
2.1.2 计算误差及修正参数 1
2.2 代码实现及结果分析 2
3 高斯判别分析 3
3.1 背景知识 3
3.2 代码实现 4
4 贝叶斯分类 4
4.1 背景知识 4
4.2 代码实现 4
5 性能分析 4
6 时效分析 4
7 影响因素分析 5
7.1 logistic 分类 5
8 总结 5
A logistic 分类代码 6
B GDA 分类代码 8
C 贝叶斯分类代码 11
D 贝叶斯库函数调用分类代码 12

1 数据集

在本次作业中, 在 UCI 中选取了 Sonar 数据集进行分类, 该数据集具有 208 个样本,
一共 60 个维度。
任务是训练网络以区分反弹的声纳信号从金属圆柱上弹下来和从大致呈圆柱形的岩石弹起。每个模式是一组 60 个数字, 范围在 0.0 到 1.0 之间。每个数字代表在特定时间段内积分的特定频段内的能量。较高频率的积分孔径在时间上较晚出现, 因为这些频率是在线性调频期间稍后传输的。如果对象是岩石,则与每个记录关联的标签包含字母 “ $\mathrm{R}$ ”,如果是地雷 (金属圆柱体) 则包含字母 “M”。标签中的数字按长宽比的高低顺序排列, 但它们不直接对角度进行编码。

2 logistic 回归与神经网络

由于 logistic 分类本质为线性求和以及激活函数的作用, 因此这里使用了神经网络框架来实现 logistic 回归, 即神经网络框架只有一个线性层, 然后使用 sigmoid 激活函数, 在结果的判定中对得到的结果进行分类, 即当结果大于 0.5 的时候为一类, 否则为另一类, 即可得出结果, 因此这两种方法同时实现了。

2.1 背景知识

2.1.1 线性及 sigmoid 函数

logistic 分类为一个线性求和和一个 sigmoid 激活组成，假设有一个 $n$ 维的输入列向量 $x$，也有一个 $n$ 维的参数列向量 $h$，还有一个偏置量 $b$ 那么就可以线性求和得到 $z_{\mathrm{s}}$：

$$
z = h^T x + b
$$

这个时候值的范围仍是 $({-}\infty, +\infty)$，无法判断出来分类，这个时候就需要一个激活函数来将值进行划分，这里使用的激活函数是 sigmoid 函数：

$$
\sigma(x) = \frac{1}{1 + e^{-x}}
$$

其导数有以下规律：

$$
\sigma’(x) = \sigma(x)(1 - \sigma(x))
$$

其图像如下图所示：

$$
a = \sigma(z) = \sigma\left( h^T x + b \right)
$$

这样进行判别，当 $a$ 大于 0.5 的时候，可以判定 $x$ 属于一类，否则属于另一类，即可进行分类。

2.1.2 计算误差及修正参数

在凸优化问题中, 可以通过导数为零进行计算。
$$\frac{\partial C}{\partial h} = 0, \quad \frac{\partial C}{\partial b} = 0$$

图 1: sigmoid 函数图像

这种直接的计算在小规模情况下可行, 但在大规模数据以及非凸优化的情况下, 采用迭代的方法得到局部最优解的方式更加可行，即如下方法：

$$
h = h - \eta \frac{\partial C}{\partial h}
$$

$$
b = b - \eta \frac{\partial C}{\partial b}
$$

其中 $\eta$ 表示学习率，这里损失函数可以使用平方差损失。即 $C = \frac{1}{2}(a - y)$，并进行迭代，即可求出结果。

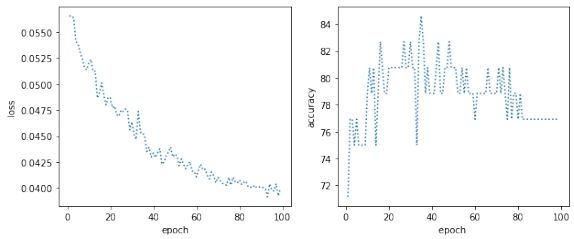
2.2 代码实现及结果分析

这里首先导入数据并将标签进行二值化, 然后利用 sklearn 来将数据进行划分, 得到训练集以及测试集。随后定义网络结构, 即仅有一个线性层并使用 sigmoid 激活函数的神经网络, 并将特征设置为数据的维度, 之后分别定义训练函数以及测试函数。然后将上文划分好的测试集以及训练集利用 TensorDataset 以及 DataLoader 得到可以送入神经网络的迭代器, 定义损失函数使用均方损失, 优化器这里使用了著名的不需要调参数的 Adadelta, 因为之前使用 SGD 的时候结果在参数调整不合适的情况会出现很大问题。最后训练并测试结果, 并将其可视化出来, 得到结果如下图所示:
又上图可知, 随着迭代次数的增多, 损失在不断下降, 而训练的精度则为先升后降的趋势,最高可以达到 (83%) 的精度。因为随着迭代次数过多,出现了过拟合的情况,使得模型在训练数据中取得的误差更小, 但是在测试数据中准确率反而不够高, 这也反映了仅使用线性网络可能导致的结果问题, 可以通过调整结果正则化以及控制迭代次数等方法来提高模型的性能。

图 2: logistic 分类结果

3 高斯判别分析

3.1 背景知识

高斯判别分析是一个比较直观的模型, 一个基本的假设就是得到的数据是独立同分布
的, 虽然这种假设在实际中很难达到, 但是在有了好的假设后可以得到较好的结果。
一维正态分布为:

$$
f(x) = \frac{1}{\sqrt{2\pi}\sigma} \exp \left( -\frac{(x - \mu)^2}{2\sigma^2} \right)
$$

其中 $x$ 为样本特征, $\sigma$ 为标准差, $\mu$ 为样本期望值，并将该分布记为 $N(\mu, \sigma^2)$，当 $\mu = 0$，$\sigma = 1$ 时候的正态分布是标准正态分布。

$n$ 维正态分布表示为：

$$
p(x; \mu, \Sigma) = \frac{1}{(2\pi)^{n/2} |\Sigma|^{1/2}} \exp\left( -\frac{1}{2} (x - \mu)^T \Sigma^{-1} (x - \mu) \right)
$$

其中 (p(x; \mu, \Sigma)) 中的 (\mu, \Sigma) 分别表示均值向量以及协方差矩阵。

将 (n) 维高斯分布应用到监督学习中，假设输入数据为 (x)，输出类别为 (y \in {0,1})，则对应分类问题可以描述为：

$$
y \approx \operatorname{Bernoulli}(\phi)
$$

$$
x | y = 0 \approx \mathcal{N}(\mu_0, \Sigma)
$$

$$
x | y = 1 \approx \mathcal{N}(\mu_1, \Sigma)
$$

其中 Bernoulli((\phi)) 表示伯努利分布，通过推导可以得出样本分类的依据：

$$
p(y | x) = \frac{p(x | y) p(y)}{p(x)}
$$

$$
y = \underset{y}{\arg\max} , p(y | x)
$$

$$
= \underset{y}{\arg\max} , p(x | y) p(y)
$$

3.2 代码实现

首先求出训练数据的均值向量以及协方差矩阵, 然后利用公式分布求出正负样本的概
率,最后将测试数据传入并与实际结果对比,得出准确率为 (75.00%) 。

4 贝叶斯分类

4.1 背景知识

贝叶斯分类是一类分类算法的总称, 一类算法以贝叶斯定理为基础, 统称为贝叶斯分类。朴素贝叶斯是贝叶斯分类中最简单常见的一种分类方法。理论上朴素贝叶斯模型比其他分类方法误差率更小, 但是由于朴素贝叶斯模型假设属性之间相互独立, 但是这个假设在实际中往往不成立, 在属性个数多或者属性相关性较大的时候, 分类效果差。朴素贝叶斯逻辑简单, 易于实现, 而且分类过程中开销比较小, 其核心算法是贝叶斯公式:
[P(B {\mid} A) = \frac{P(A {\mid} B)P(B)}{P(A)}]
其中 (A) 为特征, (B) 为类别。

4.2 代码实现

这里首先定义一个 gaussion_pdf 函数,这个函数的作用就是利用 (n) 维正态分布的公式,从而求得 (n) 维正态分布的分布情况,从而为预测函数提供概率基础,然后定义一个预测函数 predict,利用 numpy 的 unique 求得分类数,并对每一类分布,求得 (P(y)) 以及 (P(x {\mid} y)) ,最后将测试集传入,并与测试集的标签对比得出结果。
经过实践,得到准确率为 (63.46%) 。

5 性能分析

从性能上来说, 贝叶斯分类开销比较小, 而 logistic 神经网络法则比较大, 这是因为神经网络使用的空间等相对较大, 而贝叶斯由于采用的仅为样本空间, 因此性能相对较好。
从结果来说, (\operatorname{logistic}) 分类的结果在迭代次数合适的时候可以达到 (80%) 以上,高斯判别
分析可以达到 (75%) ,贝叶斯分类的准确率为 (63.46%) ,因此 logistic 效果最好。

6 时效分析

代码中已经利用了库函数 time 来计算程序运行的时间, 经过测试, logistic 分类经过 100 次迭代使用的时间为 $2.35\mathrm{\ s}$ ,而高斯判别分析用时为 $0.02\mathrm{\ s}$ ,贝叶斯分类用时 $0.01\mathrm{\ s}$ ,调用的贝叶斯分类函数,其用时同样为 $0.01\mathrm{\ s}$ 。
从时间上来说, 采用神经网络的 logistic 分类使用的轮次较多, 平均下来, 每训练一轮为 $0.02\mathrm{\ s}$ ,与高斯判别分析时间近似相等,两者都差于贝叶斯分类,自己时间的贝叶斯与库函数实现的贝叶斯时间上相差不大。
对于时间, logistic 分类每一轮都遍历一遍样本, 贝叶斯分类只遍历一次样本, 高斯判别分析需要便利每个样本的每个特征。
对于空间, logistic 分类只需用一个样本的空间, 贝叶斯分类需要有数据的类别空间, 高斯判别分析需要有正负样本的存储空间。
表 1: 时效分析

	logistic 分类	贝叶斯分类	GDA 分类
时间复杂度	$\theta(m \cdot k)$	$\theta(m)$	$\theta(m \cdot d)$
空间复杂度	$\theta(d)$	$\theta(d \cdot K)$	$\theta(d^{2})$

其中 $m$ 为样本数, $d$ 为特征维数, $k$ 为迭代次数。

7 影响因素分析

7.1 logistic 分类

在这个方法中, 我在写的过程中遇到的一个问题就是优化器的选取, 在开始使用 SGD 的时候, 损失在很短的时间就达到很大, 显示出 nan, 经过多次尝试才明白出问题的地方, 修改后, 效果较好。

8 总结

在这次的机器学习大作业中我收获很大, 这次的作用并不容易, 不仅仅要完成三个方法的分类任务, 一个重要方面是对方法的分析, 包括性能分析, 时效分析等, 这也是对能力的一次锻炼, 收获很大。

参考文献

[1] 详解朴素贝叶斯分类算法 https://blog.csdn.net/ccblogger/article/details/81712351? ivk_sa=1024320u

[2] 贝叶斯分类

[3] 高斯判别分析

A logistic 分类代码

logistic 分类.py

# -*- coding: utf-8 -*-
"""
Created on Sat Apr 10 16:56:09 2021

@author: tremble
"""

import torch
import torch.nn as nn
import torch.optim as optim
import numpy as np
import pandas as pd 
from sklearn.model_selection import train_test_split
import matplotlib.pyplot as plt
import time


start=time.time()
file=pd.read_csv('D:/桌面/sonar.csv',header=None)
data=file.iloc[:,:40]
target=file.iloc[:,-1]
data=np.array(data,dtype=float)
target=pd.get_dummies(target).iloc[:,0]
data=torch.tensor(data,dtype=torch.float)
target=torch.tensor(target,dtype=torch.float)

x_train,x_test,y_train,y_test=train_test_split(data,\
    target,test_size=0.25,random_state=5)

class logistic_net(nn.Module):
    def __init__(self,features):
        super(logistic_net,self).__init__()
        self.linear=nn.Linear(features,1)
    def forward(self,x):
        x=self.linear(x)
        x=torch.sigmoid(x)
        x = x.squeeze(-1)    
        return x
    
model=logistic_net(40)

def train(model, train_loader, optimizer, epoch, criterion):
    model.train()
    loss = 0.0
    for i, (data, target) in enumerate(train_loader):
        optimizer.zero_grad()
        output = model(data)
        loss = criterion(output, target)
        loss.backward()
        optimizer.step()
        if i % 10 == 0:
            print('Train Epoch: {} [{}/{} ({:.0f}%)]\tLoss: {:.6f}'.format(
                epoch, i * len(data), len(train_loader.dataset),
                       100. * i / len(train_loader), loss.item()))


def test(model,test_loader, criterion):
    model.eval()
    test_loss = 0
    correct = 0
    with torch.no_grad():
        for data, target in test_loader:
            pred=torch.Tensor(len(target),1)
            output = model(data)
            test_loss += criterion(output, target).item()  # sum up batch loss
            for i in range(len(target)):
                if output[i]>0.5:
                    pred[i]=torch.tensor(1)
                else:
                    pred[i]=torch.tensor(0)
            #pred = output.argmax(dim=1, keepdim=True)  # get the index of the max log-probability
            correct += pred.eq(target.view_as(pred)).sum().item()

    test_loss /= len(test_loader.dataset)

    print('\nTest set: Average loss: {:.4f}, Accuracy: {}/{} ({:.0f}%)\n'.format(
        test_loss, correct, len(test_loader.dataset),
        100. * correct / len(test_loader.dataset)))
    return test_loss,100. * correct / len(test_loader.dataset)



trainset=torch.utils.data.TensorDataset(x_train,y_train)
testset=torch.utils.data.TensorDataset(x_test,y_test)
trainloader=torch.utils.data.DataLoader(trainset,batch_size=4,shuffle=True)
testloader=torch.utils.data.DataLoader(testset,batch_size=4,shuffle=True)


criterion = nn.MSELoss()
optimizer = optim.Adadelta(model.parameters(), lr=1.0)


epoch_list,ls_list,accuracy_list=[],[],[]

for epoch in range(1, 100):
    train(model,trainloader, optimizer, epoch, criterion)
    ls,accuracy=test(model, testloader, criterion)
    epoch_list.append(epoch)
    ls_list.append(ls)
    accuracy_list.append(accuracy)

fig = plt.figure(figsize=(10,4))
plt.subplot(121)
plt.plot(epoch_list,ls_list,linestyle=':')
plt.xlabel('epoch')
plt.ylabel('loss')
plt.subplot(122)
plt.plot(epoch_list,accuracy_list,linestyle=':')
plt.xlabel('epoch ')
plt.ylabel('accuracy')
plt.show()

print('用时{:.2f}s'.format(time.time()-start))

B GDA 分类代码

GDA 分类.py

# -*- coding: utf-8 -*-
"""
Created on Sat Apr 10 18:11:49 2021

@author: tremble
"""

import numpy as np
import pandas as pd 
from sklearn.model_selection import train_test_split
import time 

start=time.time()
file=pd.read_csv('D:/桌面/sonar.csv',header=None)
data=file.iloc[:,:40]
target=file.iloc[:,-1]
data=np.array(data,dtype=float)
target=pd.get_dummies(target).iloc[:,0]

x_train,x_test,y_train,y_test=train_test_split(data,\
                target,test_size=0.25,random_state=5)


positive_data=[]
negative_data=[]
positive_num=0
negative_num=0
for (data,label)in zip(x_train,y_train):
    if label ==1:
        positive_data.append(list(data))
        positive_num+=1
    else:
        negative_data.append(list(data))
        negative_num+=1
        
row,col=np.shape(x_train)   


positive=positive_num*1.0/row
negative=1-positive
        
positive_data=np.array(positive_data)
negative_data=np.array(negative_data)        
mean_positive=np.mean(positive_data,axis=0)       
mean_negative=np.mean(negative_data,axis=0)        
positive_deta=positive_data-mean_positive
negative_deta=negative_data-mean_negative        
        
sigma=[]
for deta in positive_deta:
    deta=deta.reshape(1,col)
    ans = deta.T.dot(deta)
    sigma.append(ans)
for deta in negative_deta:
    deta=deta.reshape(1,col)
    ans = deta.T.dot(deta)
    sigma.append(ans)
sigma=np.array(sigma)
sigma=np.mean(sigma,axis=0)        
        
mean_positive=mean_positive.reshape(1,col)
mean_negative=mean_negative.reshape(1,col)        
        
def Gaussian(x,mean,cov):
    dim=np.shape(cov)[0]
    covdet = np.linalg.det(cov + np.eye(dim) * 0.001)
    covinv = np.linalg.inv(cov + np.eye(dim) * 0.001)
    xdiff = (x - mean).reshape((1, dim))
    prob = 1.0 / (np.power(np.power(2 * np.pi, dim) *\
                           np.abs(covdet), 0.5)) * \
    np.exp(-0.5 * xdiff.dot(covinv).dot(xdiff.T))[0][0]
    return prob        
        
def predict(x_test,mean_positive,mean_negetive):
    predict_label=[]
    for data in x_test:
        positive_pro=Gaussian(data, mean_positive, sigma)
        negative_pro=Gaussian(data, mean_negetive, sigma)
        if positive_pro>=negative_pro:
            predict_label.append(1)
        else:
            predict_label.append(0)
    return predict_label        
        
test_predict=predict(x_test,mean_positive,mean_negative)        
        
test_predict=np.array(test_predict)
y_test=np.array(y_test)        
        
accuracy=(test_predict==y_test).sum().item()/len(y_test)        
        
print('用时{:.2f}s,准确率为{:.2f}%'.\
      format(time.time()-start,accuracy*100.0))

C 贝叶斯分类代码

贝叶斯分类.py

# -*- coding: utf-8 -*-
"""
Created on Sat Apr 10 18:36:49 2021

@author: tremble
"""

import numpy as np
import pandas as pd 
from sklearn.model_selection import train_test_split
import time

start=time.time()
file=pd.read_csv('D:/桌面/sonar.csv',header=None)
data=file.iloc[:,:40]
target=file.iloc[:,-1]
data=np.array(data,dtype=float)
target=pd.get_dummies(target).iloc[:,0]
data=np.array(data,dtype=float)
target=np.array(target,dtype=float)
x_train,x_test,y_train,y_test=train_test_split(data,\
            target,test_size=0.25,random_state=5)

def gaussion_pdf(x_test, x):
        temp1 = (x_test - x.mean(0)) * (x_test - x.mean(0))
        temp2 = x.std(0) * x.std(0)
        return np.exp(-temp1 / (2 * temp2)) / np.sqrt(2 * np.pi * temp2)
    
def predict(x_train,y_train,x_test):
        assert len(x_test.shape) == 2
        classes = np.unique(y_train)
        pred_probs = []
        for i in classes:
            idx_i = y_train == i
            p_y = len(idx_i) / len(y_train)
            p_x_y = np.prod(gaussion_pdf(x_test,x_train[idx_i]), 1)
            prob_i = p_y * p_x_y
            pred_probs.append(prob_i)
        pred_probs = np.vstack(pred_probs)
        label_idx = pred_probs.argmax(0)
        y_pred = classes[label_idx]
        return y_pred
    
y_predict=predict(x_train,y_train,x_test)

accuracy=(y_predict==y_test).sum().item()/len(y_test)
print('准确率为{:.2f}%,用时{:.2f}s'.format(accuracy*100.0,\
                                     time.time()-start))

D 贝叶斯库函数调用分类代码

贝叶斯调用实现.py

# -*- coding: utf-8 -*-
"""
Created on Sat Apr 10 19:53:00 2021

@author: tremble
"""

from sklearn.metrics import accuracy_score
from sklearn.naive_bayes import GaussianNB
import time
import pandas as pd
import numpy as np
from sklearn.model_selection import train_test_split


start=time.time()
file=pd.read_csv('D:/桌面/sonar.csv',header=None)
data=file.iloc[:,:40]
target=file.iloc[:,-1]
data=np.array(data,dtype=float)
target=pd.get_dummies(target).iloc[:,0]
data=np.array(data,dtype=float)
target=np.array(target,dtype=float)
x_train,x_test,y_train,y_test=train_test_split(data,\
            target,test_size=0.25,random_state=5)


model = GaussianNB()
model.fit(x_train,y_train)
test_predict_model = model.predict(x_test)
print("逻辑回归的正确率为：{:.2f}%,用时为{:.2f}s".\
      format(accuracy_score(y_test,\
        test_predict_model)*100.0,time.time() - start))